
Explain why it is not a rectangle.Įxample: This figure has 4 sides and 4 vertices. Using what you know that is true of all rectangles to help you.Ĭhoose one figure you did not circle. Put a ring around all the rectangles below. They have four right angles, so they also have perpendicular line segments.Īll of the figures above are rectangles.
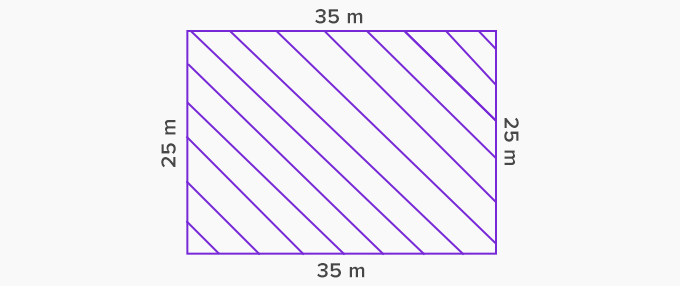
Let’s see some solved examples of properties of rectangles.All of the figures have 4 sides and 4 vertices with opposite sides parallel and congruent. Learn about Mensuration 2D Solved Examples of Properties of Rectangle The formula for the diagonal of a rectangle is derived from the Pythagoras theorem. A golden rectangle is, in other words, a rectangle whose “length to width ratio” is close to the golden ratio, which is \(1: \), where ‘l’ is the length and ‘b’ is the width of the rectangle. Golden rectangle is a shape whose sides are in a proportion equal to the golden ratio, or (a + b)/a = a/b, where “a” denotes the rectangle’s width and (a + b) its length. Golden Rectangle: Golden ratio, also known as the golden section, golden mean, or divine proportion, in mathematics, is an irrational number, often denoted by the Greek letter \(\phi\), which is approximately equal to 1.618. Diagonals are perpendicular bisectors of each other.While rectangles are not necessarily squares, all squares are rectangles. The diagonals of the square are perpendicular bisectors of each other. Along with these characteristics, a square also has equal sides where the adjacent sides make a right angle. The inner angles at each vertex of this two-dimensional form are 90 degrees. Square: An example of a rectangle is a square, which has four equal sides and four equal angles. Hence, they are the two types of rectangles. Both the Square Rectangle and the Golden Rectangle exhibit these characteristics. It has rotational symmetry around both vertical and horizontal axis.Ī rectangle has four equal sides, with the neighboring sides meeting at a 90° angle. A rectangle has two lines of symmetry.Here ∠AOB = ∠COD & ∠BOC = ∠AOD, but ∠AOB ≠ ∠AOD or ∠BOC, & ∠BOC ≠ ∠COD or ∠AOB. However, the opposite central angles are not equal but supplementary. The adjacent central angles at the point of intersection are not equal.Here diagonals AC & BD are not perpendicular to each other. The diagonals of a rectangle are not perpendicular to each other unlike that of a square.Similarly, the diagonal BD divides quadrilateral ABCD into two right-angled triangles ∆BCD and ∆BAD. In the diagram, diagonal AC divides rectangle ABCD into two right-angled triangles, ∆ABC and ∆ADC. Each diagonal divides a rectangle into two congruent right-angled triangles.The diagonals bisect each other equally i.e they intersect each other at midpoints.Here AC and BD are the diagonals & AC = BD The 2 diagonals are equal in length or congruent.The area of a rectangle is equal to the product of its length and breadth.The perimeter of a rectangle is equal to twice the sum of its length and breadth.The radius of that circle would be half of the rectangles diagonal in length. A rectangle is a cyclic quadrilateral – that is, every one of its points would fit on the edge of a circle.This is in accordance with the property of angles of a quadrilateral according to which the sum of all angles of a quadrilateral should be 360 degrees. All angles of a rectangle measure 90 degrees.The opposite sides of a rectangle are equal.The opposite sides of a rectangle are parallel.A rectangle has four sides and four vertices.This is necessary and sufficient for any polygon to be a quadrilateral.Ī list of properties of rectangles is given below: Moreover, the opposite sides of a rectangle are parallel and equal, and diagonals bisect each other. Thus, all the angles in a rectangle are equal (360°/4 = 90°). A rectangle is a quadrilateral with four right angles. Four sides, four vertices, and four angles make up the two-dimensional geometry of a rectangle.


 0 kommentar(er)
0 kommentar(er)
